Description
将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)
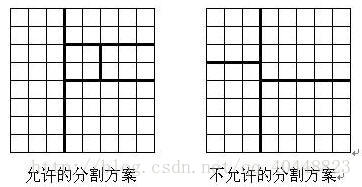
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的均方差最小。
均方差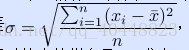
，其中平均值
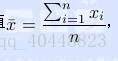，xi为第i块矩形棋盘的总分。 请编程对给出的棋盘及n，求出O’的最小值。 Input 第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。 Output仅一个数，为O’（四舍五入精确到小数点后三位）。
Sample Input3
1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 3 Sample Output1.633
SourceNoi 99
》》》
这是一道区间dp，首先先要将所求的式子进行化简，我们先把每一项展开(Xi-x)^2=Xi^2 - 2*Xi*x+x^2然后n项的和就是(X1^2+X2^2…….+Xn^2)-(2X1x+2X2x……..+2Xnx)+nx^2.
因为X1+X2+….+Xn为矩阵的总权值和，就等于x*n
所以(2X1x+2X2x……..+2Xnx)=2*x*n*x
所以原式就可以变为：(X1^2+X2^2…….+Xn^2)-nx^2
得到σ^2=1/n∑xi^2 - x^2。
所以要使得方差最小只要使得∑xi^2最小就可以了。
之后再思考状态转移方程用一个五维数组dp[x1][y1][x2][y2][k]来表示在进行k次分割后还剩的左上角坐标为（x1,y1），右下角坐标为（x2,y2）的最小平方和。
再枚举x1,x2,y1,y2,k与横向或竖向分割的边aa，则有dp[i][j][xx][yy][k]=min(dp[i][j][xx][yy][k],dp[i][j][aa][yy][k-1]+dp[aa+1][j][xx][yy][0]);dp[i][j][xx][yy][k]=min(dp[i][j][xx][yy][k],dp[aa+1][j][xx][yy][k-1]+dp[i][j][aa][yy][0]);dp[i][j][xx][yy][k]=min(dp[i][j][xx][yy][k],dp[i][aa+1][xx][yy][k-1]+dp[i][j][xx][aa][0]);dp[i][j][xx][yy][k]=min(dp[i][j][xx][yy][k],dp[i][j][xx][aa][k-1]+dp[i][aa+1][xx][yy][0]);
预处理是用容斥原理记录一个sum[i][j]，表示（i,j）这个点到原点的矩阵权值和，然后在算出dp[x1][y1][x2][y2][0]的值（也就是没有被分割时的值）。
细节处理较多，上代码
#include#include #include #include using namespace std;const int N=10;int n,dp[N][N][N][N][2*N],a[N][N],x,sumall,sum[N][N];inline int s(int x1,int y1,int x2,int y2){ //预处理 int now=sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][y1-1]; return now;}int main(){ while(~scanf("%d",&n)){ for(int i=1;i<=8;i++) for(int j=1;j<=8;j++) scanf("%d",&a[i][j]),sumall+=a[i][j]; for(int i=1;i<=8;i++) for(int j=1;j<=8;j++) sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]; for(int i=1;i<=8;i++) for(int j=1;j<=8;j++) for(int x=i;x<=8;x++) for(int y=j;y<=8;y++) dp[i][j][x][y][0]+=s(i,j,x,y), dp[i][j][x][y][0]*=dp[i][j][x][y][0]; for(int k=1;k
时间复杂度大概是O（8^5*n） 空间复杂度是O（8^4*n）。